1. The first indication of the phenomenon.-- When we consider a fluid mass in equilibrium, for example, some water in a glass, all the parts of the mass appear completely motionless to us. If we put into it an object of greater density it falls and, if it is spherical, it falls exactly vertically. The fall, it is true, is the slower the smaller the object; but, so long as it is visible, it falls and always ends by reaching the bottom of the vessel. When at the bottom, as is well known, it does not tend again to rise, and this is one way of enunciating Carnot's principle (impossibility of perpetual motion of the second sort).
These familiar ideas, however, only hold good for the scale of size to which our organism is accustomed, and the simple use of the microscope suffices to impress on us new ones which substitute a kinetic for the old static conception of the fluid state.
Indeed it would be difficult to examine for long preparations in a liquid medium without observing that all the particles situated in the liquid instead of assuming a regular movement of fall or ascent, according to their density, are, on the contrary, animated with a perfectly irregular movement. They go and come, stop, start again, mount, descend, remount again, without in the least tending toward immobility. This is the Brownian movement, so named in memory of the naturalist Brown, who described it in 1827 (very shortly after the discovery of the achromatic objective), then proved that the movement was not due to living animalculae, and recognised that the particles in suspension are agitated the more briskly the smaller they are.
2. Projection of the Brownian movement-- This phenomenon can be made visible to a whole audience by projection, but this is difficult, and it may be useful to detail the precautions which have enabled me to arrive at a satisfactory result. The image of an electric arc (or better, the sun) is formed in the preparation, the greater part of the non-luminous heat rays being stopped by means of a cell full of water. The rays, reflected by the particles in suspension, traverse, as for direct observation, an immersion objective and an eyepiece of high magnification, and are then turned horizontally by a total-reflection prism so as to form the image of the granules on a screen of ground glass (ruled in squares by preference, so as to have reference marks), on the farther side of which the audience is. The light is thus better utilised than with an ordinary screen which would diffuse a large part of it in directions where there were no observers. The magnification can be usefully raised to 8,000 or 10,000 diameters.
But it is necessary above all to procure an appropriate emulsion. In the few trials of projection which have been made up till now, the diameter of the granules employed was of the order of a micron, and their image is visible only with difficulty beyond 3 metres (at least with the light of the arc) whether immersion or lateral illumination is used. Smaller granules are still less visible, and one is led to this, at first sight, paradoxical conclusion, that it is better to project large granules than small ones. It is true that their movement is less, but it is still quite sufficient for its essential characteristics to be easily recognised.
It is still necessary to know how to prepare particles having a diameter of several microns, and we shall see soon that this is equally desirable in regard to certain points in the experimental study proper of the Brownian movement. I shall indicate later (No. 32) how I have succeeded in obtaining large, perfectly spherical granules of gamboge and mastic. With such granules the Brownian movement can still be perceived at a distance of 8 or 10 metres from the screen in a hall which has been made absolutely dark.
3. Persistence of the phenomenon in absence of all causes external to the fluid. Its explanation by the movements of molecules.-- The singular phenomenon discovered by Brown did not attract much attention. It remained, moreover, for a long time ignored by the majority of physicists, and it may be supposed that those who had heard of it thought it analogous to the movement of the dust particles, which can be seen dancing in a ray of sunlight, under the influence of feeble currents of air which set up small differences of pressure or temperature. When we reflect that this apparent explanation was able to satisfy even thoughtful minds, we ought the more to admire the acuteness of those physicists, who have recognised in this, supposed insignificant, phenomenon a fundamental property of matter.
Besides, as happens most frequently when it is sought to unravel the genesis of a great directing idea, it is difficult to fix precisely how the hypothesis, which ascribes the Brownian movement to molecular agitation, first appeared and how it was developed.
The first name which calls for reference in this respect is, perhaps, that of Weiner, who declared at the conclusion of his observations, that the movement could not be due to convection currents, that it was necessary to seek for the cause of it in the liquid itself, and who, finally, almost at the commencement of the development of the kinetic theory of heat, divined the molecular movements were able to give the explanation of the phenomenon.[1]
Some years later Fathers Delsaulx and Carbonnelle published in the Royal Microscopical Society and in the Revue des Questions scientifiques, from 1877 to 1880, various Notes on the Thermodynamical Origin of the Brownian Movement[2]. In a note by Father Delsaulx, for example, one may read: "the agitation of small corpuscles in suspension in liquids truly constitutes a general phenomenon," that it is "henceforth natural to ascribe a phenomenon having this universality to some general property of matter," and that "in this train of ideas, the internal movements of translation which constitute the calorific state of gases, vapours and liquids, can very well account for the facts established by experiment."
In another Note, by Father Carbonnelle, one, again, may read this: "In the case of a surface having a certain area, the molecular collisions of the liquid which cause the pressure, would not produce any perturbation of the suspended particles, because these, as a whole, urge the particles equally in all directions. But if the surface is of area less than is necessary to ensure the compensation of irregularities, there is no longer any ground for considering the mean pressure; the inequal pressure, continually varying from place to place, must be recognised, as the law of large numbers no longer leads to uniformity; and the resultant will not now be zero but will change continually in intensity and direction. Further, the inequalities will become more and more apparent the smaller the body is supposed to be, and in consequence the oscillations will at the same time become more and more brisk. ..."
These remarkable reflections unfortunately remained as little known as those of Weiner. Besides it does not appear that they were accompanied by an experimental trial sufficient to dispel the superficial explanation indicated a moment ago; in consequence, the proposed theory did not impress itself on those who had become acquainted with it.
On the contrary, it was established by the work of M. Gouy (1888), not only that the hypothesis of molecular agitation gave an admissible explanation of the Brownian movement, but that no other cause of the movement could be imagined, which especially increased the significance of the hypothesis.[3] This work immediately evoked a considerable response, and it is only from this time that the Brownian movement took a place among the important problems of general physics.
In the first place, M. Gouy observed that the Brownian movement is not due to vibrations transmitted to the liquid under examination, since it persists equally, for example, at night on a sub-soil in the country as during the day near a populous street where heavy vehicles pass. Neither is it due to the convection currents existing in fluids where thermal equilibrium has not been attained, for it does not appreciably change when plenty of time is given for equilibrium to be reached. Any comparison between Brownian movement and the agitation of dust-particles dancing in the sunlight must therefore be set aside. In addition, in the latter case, it is easy to see that the neighbouring dust-particles move in general in the same sense, roughly tracing out the form of the common current which bears them along, whereas the most striking feature of the Brownian movement is the absolute independence of the displacements of neighbouring particles, so near together that they pass by one another. Lastly, neither can the unavoidable illumination of the preparation be suspected, for M. Gouy was able abruptly to reduce it a thousand times, or to change its colour considerably, without at all modifying the phenomenon observed. All the other causes from time to time imagined have as little influence; even the nature of the particles does not appear to be of any importance, and henceforward it was difficult not to believe that these articles simply serve to reveal an internal agitation of the fluid, the better the smaller they are, much as a cork follows better than a large ship the movements of the waves of the sea.
Thus comes into evidence, in what is termed a fluid in equilibrium, a property eternal and profound. This equilibrium only exists as an average and for large masses; it is a statistical equilibrium. In reality the whole fluid is agitated indefinitely and spontaneously by motions the more violent and rapid the smaller the portion taken into account; the statical notion of equilibrium is completely illusory.
4. Brownian movement and Carnot's principle.-- There is therefore an agitation maintained indefinitely without external cause. It is clear that this agitation is not contradictory to the principle of the conservation of energy. It is sufficient that every increase in the speed of a granule is accompanied by a cooling of the liquid in its immediate neighbourhood, and likewise every decrease of speed by a local heating, without loss or gain of energy. We perceive that thermal equilibrium itself is also simply a statistical equilibrium. But it should be noticed, and this very important idea is again due to M. Gouy, that the Brownian movement is not reconcilable with the rigid enunciations too frequently given to Carnot's principle; the particular enunciation chosen can be shown to be of no importance. For example, in water in equilibrium it is sufficient to follow with the eyes a particle denser than water to see it at certain moments rise spontaneously, absorbing, necessarily, work at the expense of the heat of the surrounding medium. So it must not any longer be said that perpetual motion of the second sort is impossible, but one must say: "On the scale of size which interests us practically, perpetual motion of the second sort is in general so insignificant that it would be absurd to take it into account." Besides such restrictions have long been laid down: the point of view that Carnot's principle expresses simply a law approximated to has been upheld by Clausius, Maxwell, Helmholtz, Boltzmann, and Gibbs, and in particular may be recalled the demon, imagined by Maxwell, which, being sufficiently quick to discern the molecules individually, made heat pass at will from a cold to a hot region without work. But since one is limited to the intervention of invisible molecules, it remained possible, by denying their existence, to believe in the perfect rigidity of Carnot's principle. But this would no longer be admissible, for this rigidity is now in opposition to a palpable reality.
On the other hand, the practical importance of Carnot's principle is not attacked, and I hardly need state at length that it would be imprudent to count upon the Brownian movement to lift the stones intended for the building of a house. But the comprehension of this important principle becomes in consequence more profound: its connection with the structure of matter is better understood, and the conception is gained that it can be enunciated by saying that spontaneous co-ordination of molecular movements becomes the more improbable the greater the number of molecules and the greater the duration of time under consideration[4].
5. The kinetic molecular hypothesis.-- I have said that the Brownian movement is explained, in the theory of M. Gouy and his predecessors, by the incessant movement of the molecules of the fluid, which striking unceasingly the observed particles, drive about these particles irregularly through the fluid except in the case where these impacts exactly counterbalance one another. It has, to be sure, been long recognised, especially in explanation of the facts of diffusion, and of the transformation of motion into heat, not only that substances in spite of their homogeneous appearance, have a discontinuous structure and are composed of separate molecules, but also that these molecules are in incessant agitation, which increases with the temperature and only ceases at absolute zero.
Instead of taking this hypothesis ready made and seeing how it renders account of the Brownian movement, it appears preferable to me to show that, possibly, it is logically suggested by this phenomenon alone, and this is what I propose to try.
What is really strange and new in the Brownian movement is, precisely, that it never stops. At first that seems in contradiction to our every-day experience of friction. If for example, we pour a bucket of water into a tub, it seems natural that, after a short time, the motion possessed by the liquid mass disappears. Let us analyse further how this apparent equilibrium is arrived at: all the particles had at first velocities almost equal and parallel; this co-ordination is disturbed as soon as certain of the particles, striking the walls of the tub, recoil in different directions with changed speeds, to be soon deviated anew by their impacts with other portions of the liquid. So that, some instants after the fall, all parts of the water will be still in motion, but it is now necessary to consider quite a small portion of it, in order that the speeds of its different points may have about the same direction and value. It is easy to see this by mixing coloured powders into a liquid, which will take on more and more irregular relative motions.
What we observe, in consequence, so long as we can distinguish anything, is not a cessation of the movements, but that they become more and more chaotic, that they distribute themselves in a fashion the more irregular the smaller the parts.
Does this de-co-ordination proceed indefinitely?
To have information on this point and to follow this de-co-ordination as far as possible after having ceased to observe it with the naked eye, a microscope will be of assistance, and microscopic powders will be taken as indicators of the movement. Now these are precisely the conditions under which the Brownian motion is perceived: we are therefore assured that the de-co-ordination of motion, so evident on the ordinary scale of our observations, does not proceed indefinitely, and, on the scale of microscopic observation, we establish an equilibrium between the co-ordination and the de-co-ordination. If, that is to say, at each instant, certain of the indicating granules stop, there are some in other regions at the same instant, the movement of which is re-co-ordinated automatically by their being given the speed of the granules which have come to rest. So that it does not seem possible to escape the following conclusion:
Since the distribution of motion in a fluid does not progress indefinitely, and is limited by a spontaneous re-co-ordination, it follows that the fluids are themselves composed of granules or molecules, which can assume all possible motions relative to one another, but in the interior of which dissemination of motion is impossible. If such molecules had no existence it is not apparent how there would be any limit to the de-co-ordination of motion.
On the contrary if they exist there would be, unceasingly, partial re-co-ordination; by the passage of one near another, influencing it (it may be by impact or in any other manner), the speeds of these molecules will be continuously modified in magnitude and direction, and from these same chances it will come about sometimes that neighbouring molecules will have concordant motions. In addition, even without this absolute concordance being necessary, it will at least come about frequently that the molecules in the region of an excess of motion sufficient to drive the particle in that direction.
The Brownian movement is permanent at constant temperature: that is an experimental fact. The motion of the molecules which it leads us to imagine is thus itself also permanent. If these molecules come into collision like billiard balls, it is necessary to add that they are perfectly elastic, and this expression can, indeed, be used to indicate that in the molecular collisions of a thermally isolated system the sum of the energies of motion remains definitely constant.
In brief the examination of Brownian movement alone suffices to suggest that every fluid is formed of elastic molecules, animated by a perpetual motion.
6. The atoms. Avogadro's constant.-- From this, as is well known, diverse considerations of chemistry, and particularly the study of substitution, lead to the idea of the existence of atoms. When, for example, calcium is dissolved in water, only one half of the hydrogen contained in the latter is displaced. The hydrogen of this water, and in consequence the hydrogen of each molecule, is therefore composed of two distinct parts. No experiments lead to any further differentiation, and it is reasonable to regard these two parts as indivisible, by all chemical methods, or in a word, they are atoms. On the other hand, every mass of water, and in consequence each molecule of water, weighs 9 times the hydrogen it contains: the molecule of water, which contains 2 atoms of hydrogen, weighs therefore 18 times the atom of hydrogen. In a similar manner, it may be established that the molecule of methane, for example, weighs 16 times more than the atom of hydrogen. Thus, by a purely chemical method, through the conception of the atom, the ratio 16/18, of the weight of a molecule of methane to a molecule of water, can be reached.
Now this same ratio, precisely, is arrived at by comparison of the masses of similar volumes of methane and water vapour in the gaseous state under similar conditions of temperature and pressure. Thus these two masses, which have the same ratio as the two kinds of molecules, must contain as many molecules the one as the other. This result is general for the different gases, so that in consequence we arrive, in an experimental manner, at the celebrated proposition enunciated in the form of an hypothesis by Avogadro, about a century ago, and taken up again a little later by Ampère:
"Any two gases, taken under the same conditions of temperature and pressure, contain in the same volume the same number of molecules."
It has become customary to name as the gram-molecule of a substance, the mass of the substance which in the gaseous state occupies the same volume as 2 grams of hydrogen measured at the same temperature and pressure. Avogadro's proposition is then equivalent to the following:
"Any two gram-molecules contain the same number of molecules."
This invariable number N is a universal constant, which may appropriately be designated Avogadro's Constant. If this constant be known, the mass of any molecule is known: even the mass of any atom will be known, since we can learn by the different methods which lead to chemical formulae, how many atoms of each sort there are in each molecule. The weight of a molecule of water, for example, is 18/N; that of a molecule of oxygen is 32/N, and so on for each molecule. Similarly the weight of the oxygen atom, obtained by dividing the gram-atom of oxygen by N, is 16/N; that of the atom of hydrogen is 1.008/N, and so on for each atom.[5]
...
Let us now consider a particle a little larger still, itself formed of several molecules, in a word a dust. Will it proceed to react toward the impact of the molecules encompassing it according to a new law? Will it not comport itself simply as a very large molecule, in the sense that its mean energy has still the same value as that of an isolated molecule? This cannot be averred without hesitation, but the hypothesis at least is sufficiently plausible to make it worth while to discuss its consequences.
Here we are then taken back again to the observation of the particles of an emulsion and to the study of this wonderful movement which most directly suggests the molecular hypothesis. But at the same time we are led to render the theory precise by saying, not only that each particle owes its movement to the impacts of the molecules of the liquid, but further that the energy maintained by the impacts is on the average equal to that of any one of these molecules. ... We are led to regard the mean energy of translation of a molecule as equal to that possessed by the granules of an emulsion.
A closer examination confirms this conception and gives the law of rarefaction. ...
Let us imagine a uniform emulsion in equilibrium, which fills a vertical cylinder of cross section s. The state of a horizontal slice contained between the levels of h and h + dh would not be changed if it were enclosed between two pistons, permeable to the molecules of water, but impermeable to the granules (membranes of parchment-paper or of collodion could effectively play this part). Each of these semi-permeable pistons is subjected to the impact of the granules which it stops to an osmotic pressure. If the emulsion is dilute, this pressure can be calculated by the same reasoning as for a gas or a dilute solution, in the sense that, if at level h there are n granules per unit volume, the osmotic pressure P will be equal to 2/3nW, if W signifies the mean granular energy; it will be 2/3(n+dn)W at the level h + dh. Now the slice of granules under consideration does not fall: for this it is necessary that there should be equilibrium between the difference of the osmotic pressures, which urges it upward, and the total weight of the granules, diminished by the buoyancy of the liquid, which urges them downwards. Hence, calling φ the volume of each granule, Δ its density, and δ that of the intergranular liquid, we see that
-(2/3)sW dn = ns dh φ(Δ-δ)g ,or
-(2/3)W dn/n = φ(Δ-δ)g . dh ,which, by an obvious integration, involves the following relation between the concentrations n0 and n at two points for which the difference of level is h:
(2/3)W log (n0/n) = φ(Δ-δ)gh ,a relation which may be termed the equation of distribution of the emulsion. It shows clearly that the concentration of the granules of a uniform emulsion decreases in an exponential manner as a function of the height, in the same way as the barometric pressure does as a function of the altitude.[6]
If it is possible to measure the magnitudes other than W which enter into this equation, one can see whether it is verified and whether the value it indicates for W is the same as that which has been approximately assigned to the molecular energy. In the event of an affirmative answer, the origin of the Brownian movement will be established, and the laws of gases, already extended by Van't Hoff to solutions, can be regarded as still valid even for emulsions with visible granules.
I have made some trials without result upon these colloidal solutions (sulfate of arsenic, ferric hydroxide, collargol, etc.). On the other hand, after some trials, I have been enabled to carry out measurements on emulsions of gamboge, then (with the assistance of M. Dabrowski) on emulsions of mastic.
The gamboge, which is used for a water-colour, comes from the desiccation of the latex secreted by Garcinia morella (guttier of Indo-China). A piece of this substance rubbed with the hand under a thin film of distilled water (as soapsuds can be made from a piece of soap) dissolves little by little, giving a beautiful opaque emulsion of a bright yellow colour, in which the microscope shows a swarm of yellow granules of various sizes, all perfectly spherical. These yellow granules can be separated from the liquid in which they are contained by energetic centrifuging, in the same manner as the red corpuscles may be separated from blood serum. They then collect at the bottom of the vessel centrifuged as a yellow mud, above which is a cloudy liquid which is decanted away. The yellow mud diluted anew (by shaking) with distilled water gives the mother emulsion which will serve for the preparation of the uniform emulsions intended for the measurements.
Instead of so using the natural granules the gamboge may be treated with methyl alcohol which entirely dissolves the yellow material (about four-fifths of the raw material) leaving a mucilaginous residue, to the properties of which I shall perhaps have to revert. This alcoholic solution, which is quite transparent and very similar to a solution of bichromate, changes suddenly, on the addition of much water, into a yellow opaque emulsion of the same appearance as the natural emulsion, and like it, composed of spherical granules. They can be separated again by centrifuging from the weak alcoholic liquid which contains them, then diluted with pure water, which gives, as in the preceding case, a mother emulsion which consists of granules of very different sizes. ...
[Several sections dealing with the preparation of emulsions containing particles of uniform size and the determination of their density are omitted. --Boorse & Motz]
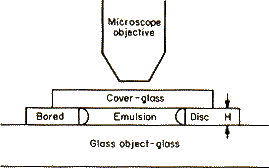
Let us suppose that a very thin glass plate border with a large hole has been cemented in a fixed position upon a glass slide [Figure]. Thus will be formed a shallow cylindrical vessel of which the height H will be, for example, about 100 μ (0.1 mm).[7]

At the centre of this vessel is placed a drop of the emulsion, which is immediately flattened by the cover-glass, and the latter, sticking to the upper face of the perforated glass plate, completely closes the cell. In addition, to prevent all evaporation, the edges of the cover-glass are covered with paraffin or varnish, which admits of a preparation being kept under observation during several days or even weeks.
The preparation is then put on to the stage of a good microscope, which has been carefully levelled. The objective used, being of a very high magnifying power, has a small depth of focus, and only those granules can be seen clearly at the same time which are present in a very thin horizontal layer, the thickness of which is of the order of a micron. By raising or lowering the microscope the granules in another layer can be seen.
The vertical distance between these two layers corresponds to a height h which enters into the equation of distribution, and this must be exactly known. We obtain it by multiplying the displacement h' of the microscope by the relative refractive index of the two media which the cover-glass separates. As the intergranular liquid is water, h will be equal to (4/3)h', if a dry objective is employed, and simply equal to h' if, as I have most frequently done, a water immersion is used. As for the displacement h', it is read off directly on the granulated disc, fixed to the micrometer screw actuating the motion of the microscope (the screw of the Zeiss instrument reads to at least the quarter of a micron).
That does not at first sight appear to be easy: it is not a question of counting fixed objects, and when the eye is placed to the microscope and some hundreds of granules are seen moving in every direction, besides disappearing unceasingly while at the same time new granules make their appearance, one is soon convinced of the uselessness of attempts to estimate even roughly the mean number of granules present in the layer under observation.
The simplest course appears to be to take instantaneous photographs of this layer, to obtain the number of sharp images of granules there, and, if the emulsion is so dilute that the number is small, to repeat the process until the mean number of granules obtained on the plate can be considered known to the desired degree of approximation, for example, 1 per cent. I have, indeed, employed this procedure for the relatively large granules, as will appear later. For granules of diameter less than 0.5 μ I have not been able to obtain good images, and I have had recourse to the following device: I placed in the focal plane of the eyepiece an opaque screen of foil pierced with a very small round hole by means of a dissecting-needle. The field of vision is thus very much diminished, and the eye can take in at a glance the exact number of granules visible at a definite instant, determined by a short signal, or during the very short period of illumination which can be obtained by means of a photographic shutter. It is necessary for this that the number does not exceed 5 or 6.
Operating thus at regular intervals, every 15 seconds for example, a series of numbers is noted down of which the mean value approaches more and more nearly a limit which gives the mean frequency of granules at the level studied, in the small cylindrical layer upon which the microscope is set. Recommencing at another level, the mean frequency is there redetermined for the same volume, and the quotient of these two numbers gives the ratio of the concentrations sought. As well understood, instead of making all the readings relating to one level continuously it is better to alternate the readings, making for example 100 at one level, then 100 at another level, then again 100 at the first level, and so on.
Some thousands of readings are required if some degree of accuracy is aimed at. To take an example, I have copied below the numbers given by 50 consecutive readings at two levels 30 μ apart in one of the emulsions I have used:
| 3 | 2 | 0 | 3 | 2 | 2 | 5 | 3 | 1 | 2 |
| 3 | 1 | 1 | 0 | 3 | 3 | 4 | 3 | 4 | 4 |
| 0 | 3 | 1 | 3 | 1 | 4 | 2 | 2 | 1 | 3 |
| 1 | 1 | 2 | 2 | 3 | 0 | 1 | 3 | 4 | 3 |
| 0 | 2 | 2 | 1 | 0 | 2 | 1 | 3 | 2 | 4 |
| 2 | 1 | 0 | 0 | 1 | 1 | 3 | 1 | 0 | 0 |
| 0 | 2 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 0 |
| 2 | 1 | 3 | 3 | 1 | 0 | 0 | 0 | 3 | 0 |
| 1 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 2 | 4 | 1 | 0 | 1 | 0 | 1 |
This radius would be obtained in a very certain manner, if it were possible to find how many granules (immediately after shaking) there were in a known titrated volume of emulsion. That would give the mass of a granule and in consequence, since its density is known, the radius. It would be sufficient for this to count all the granules present in a cylinder of the emulsion having, as height, the height of the preparation (about 100 μ) and, as base, a surface of known area, engraved previously on the microscope slide, which is done in the cells for the enumeration of corpuscles, the bottom of which is divided into squares of 50 μ side. But the counting (or integration), layer by layer, of all the granules present in the height of the preparation carries with it much uncertainty. It is necessary in fact to know exactly the depth of each layer, which is of the order of a micron,[8] not to speak of other difficulties.
Happily I have had occasion in another connection to notice that in a feebly acid medium (for example 0.01 gram-molecule per litre) the granules of gamboge or of mastic collect on the walls of the glass which holds the preparation. At a perceptible distance from the walls the Brownian movement is in no way modified; but as soon as the chances of the movement bring a granule into contact with the slide or cover-glass, the granule becomes motionless and does not leave the wall. The emulsion is thus progressively impoverished and, after some hours, all the granules it contained are affixed to the walls. Only those, however, can be counted which are fixed in distinct positions and which to not form part of a clotted mass (partial coagulation of the colloid). Without being able to insist upon it here, I am content to say that the very minute quantities of a protecting colloid, precisely such as is present in the natural latex of gamboge, added to the emulsion studied, prevent the granules from caking together in water acidulated by pure hydrochloric acid. On this account one may operate as follows:--
The uniform emulsion under observation, which has been previously titrated, is shaken, and a known volume of it is mixed with a known volume of feebly acidulated water, and again shaken: a drop of the mixture is taken and arranged on the microscope slide, and at once flattened by a cover-glass, the edges of which are then paraffined, taking care not to displace it, for all parts at first moistened and then abandoned by the liquid carry away the granules. This done, the preparation is left on the stage of the microscope until all the granules have become attached to the walls. A camera lucida is then fitted to the microscope and, focussing on the bottom of the preparation, the contour which corresponds to one of the squares engraved upon the slide is drawn: the image of each of the granules fixed inside this square is marked by a point: then, adjusting the microscope until the granules fixed to the upper face are sharply defined, the images of these granules within the same contour are marked in the same way, which correspond in consequence to the same right prism of emulsion. The points on the drawing obtained can be subsequently counted at leisure, and their number is equal to the number of granules sought.
The same work is then recommenced upon another portion of the preparation, and soon until the mean value of the number of granules marked in each square can be considered well known. An obvious calculation then permits the number of granules contained in unit volume of the primary titrated emulsion to be found and gives in consequence the required radius, by a second method into which the law of Stokes does not enter. ...
The use of the camera lucida, fatiguing in other respects, would have been avoided by directly photographing the granules fixed to the walls. But the eye is more sensitive than the photographic plate as regards the visibility of very small clear granules on a bottom almost equally clear (it must not be forgotten that the granules are transparent spheres), and I have only been able to employ photography for granules having a diameter exceeding a demimicron.
This is just what experiment verifies. At first practically as many granules are visible in the upper layers as in the lower layers of the emulsion. A few minutes suffice for the lower layers to become manifestly richer in granules than the upper layers. If then the counting of the granules at two different levels is commenced, the ratio n0/n of the concentrations at these levels is found to have a value gradually increasing for some time, but more and more slowly, and which ends by showing no systematic variation. With the emulsions I have employed three hours is sufficient for the attainment of a well-defined limiting distribution in an emulsion left at rest, for practically the same values are found after 3 hours as after 15 days. Those emulsions which have not been rendered aseptic are occasionally invaded by elongated and very active protozoa, which, by stirring up the emulsion like fishes agitating the mud of a pond, much diminish the inequality of the distribution between the upper and lower layers. But if one has patience to wait until these microbes, through lack of food, die and fall inert to the bottom of the preparation, which takes two or three days, it will be found that the initial limiting redistribution is exactly regained, and this possesses all the characters of the distribution of a permanent regime.
Once this permanent state is attained, it is easy to see whether the concentration decreases in an exponential manner as a function of the height. The following measurements show that it is so.
At first I worked on granules of gamboge of radius approximately equal to 0.14 μ, which were studied in a cell having a height of 110 μ. The concentrations of the granules were determined in five equidistant planes, the lowest plane being taken 5 μ above the bottom of the preparation (to eliminate the possible influence of the boundary), the distance between two consecutive planes being 25 μ, so that the uppermost plane was 5 μ below the surface.
The numbers found were between themselves as
100, 116, 146, 170, 200,
whereas the numbers
100, 119, 142, 169, 201,
which do not differ from the preceding by more than the limits of experimental error, are in geometrical progression. The distribution of the granules is thus quite exponential, as is the case for a gas in equilibrium under the influence of gravity. Only the diminution of the concentration to one-half, which for the atmosphere is produced by a height of about 6 kilometres, is produced here in a height of 0.1 millimetre.
But this fall of concentration is still too feeble for the exponential character of the decrease to be quite manifest. I have therefore tried to secure with larger granules a more rapid fall of concentration.
My most careful series has been done with granules of gamboge having a radius of 0.212 μ. The readings have been made, in a cell having a height of 100 μ, in four equidistant horizontal planes cutting the vessel at the levels
5 μ, 35 μ, 65 μ, 95 μ.
These readings, made by direct counting through a needle-hole, relate to 13,000 granules and give, respectively for these levels, concentrations proportional to the numbers
100, 47, 22.6, 12,
which are practically equal to the numbers
100, 48, 23, 11.1,
which again are exactly in a geometrical progression.
Thus the exponential distribution cannot be doubted, each elevation of 30 μ here decreasing the concentration to about half its value.
It may be interesting to observe that the largest of the granules, for which I have found the laws of perfect gases followed, are already visible in sunlight under a strong lens. They behave as the molecules of a perfect gas, of which the gram-molecule would weigh 200,000 tons.
2.303 RT/N log10 n0/n = (4/3) πa3g(Δ-δ)h .
Once this has been well established, this same equation affords a means for determining the constant N, and the constants depending upon it, which is, it appears, capable of an unlimited precision. The preparation of a uniform emulsion and the determination of the magnitudes other than N which enter into the equation can in reality be pushed to whatever degree of perfection desired. It is simply a question of patience and time; nothing limits a priori the accuracy of the results, and the mass of the atom can be obtained, if desired, with the same precision as the mass of the Earth. I scarcely need observe, on the other hand, that even perfect measurements of compressibility might not be able to prevent an uncertainty of perhaps 40 per cent. in the value of N, deduced from the equation of Van der Waals, by means of hypotheses which we know are certainly not completely exact.
The values found for N by the five series of experiments detailed give a rough mean of 69.1022; the most careful of the series is the one made with mastic (dotting upon photographic plates) which gives 70.1022.
I have made, with gamboge, a sixth series already mentioned above on various occasions, which I consider considerably more accurate still. The mean radius of the granules of the emulsion employed was found equal to 0.212 μ, by counting 11,000 granules of a titrated emulsion, and to 0.213 μ by application of the law of Stokes. The difference of density between the material of the granules and the intergranular water was 0.2067 at 20°, the temperature to which the measurements refer. 13,000 granules were counted at different heights (direct observation through a needle-hole), and it was verified that the distribution was quite exponential, each elevation of 30 μ lowering the concentration to about half of its value (exact figures are given in No. 22). The value resulting from these measurements is 70.5 x 1022. ... Thus, then, one is led to adopt for Avogadro's constant the value
N = 70.5 x 1022.
[2]See for this bibliography an article which appeared in the Revue des Questions scientifiques, January 1909, where M. Thirion very properly calls attention to the ideas of these savants, with whom he collaborated. [original note]
[3]Journal de Physique, 1888, 2nd Series, vii. 561; Comptes rendus, 1889, cix. 102; Revue générale des Sciences, 1895, 1. [original note]
[4]With regard to the general significance of the principle I should refer to the very interesting considerations developed by J. H. Rosny, Senior, in his book on Pluralism, pp. 85-91 (F. Alcan, 1909). [original note]
[5]From here on, Boorse & Motz's excerpt. --CJG
[6]I indicated this equation at the time of my first experiments (Comptes rendus, May 1908). I have since learnt that Einstein and Smoluchowski, independently, at the time of their beautiful theoretical researches of which I shall speak later, had already seen that the exponential distribution is a necessary consequence of the equipartition of energy. Beyond this it does not seem to have occurred to them that in this sense an experimentum crucis could be obtained, deciding for or against the molecular theory of the Brownian movement.
[7]These requirements are quite satisfied by the cells for enumeration of the blood corpuscles (Zeiss), which I have employed.
[8]We do not need to know this thickness when, in order to obtain the ratio of the concentrations at two different levels, we take the ratio of the number of granules visible at these two levels: it is sufficient for our purpose that the depth of the field, whatever it may be, has the same value for these two levels.
 Back to the list of selected historical papers.
Back to the list of selected historical papers. Back to the top of Classic Chemistry.
Back to the top of Classic Chemistry.